Отток клиентов (churn) — интересная проблема. Вычислить его фактическое значение несложно. Но как только вы начинаете составлять прогноз на будущее, расчет становится заметно труднее.
Часто маркетологи определяют и прогнозируют отток по-разному. Попробуем разобраться с многочисленными способами и выбрать оптимальный. Для начала ответим на вопрос: что такое отток?
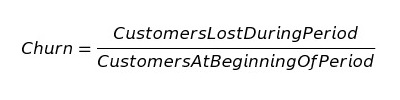
где:
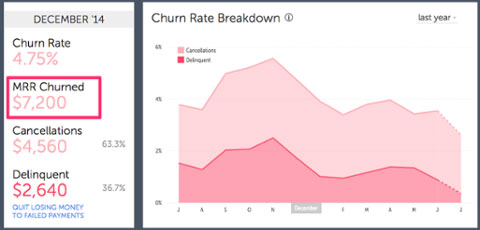
Customer Lost During Period — количество покупателей, покинувших вас за период
Customers At Beginning Of Period — общее количество покупателей на начало периода
К примеру, на начало января у вас было 100 клиентов. За месяц вы потеряли 10 из них. Показатель оттока за январь будет равен 10%.
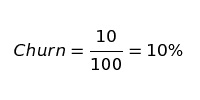
Это дескриптивная модель оттока. Она дает понять, что произошло, но ее возможности ограничены в случае, если нам интересна тенденция изменения показателя. Единственное, что мы можем сказать, опираясь на эту формулу: «Мы потеряли 10% клиентов в этом месяце».
Дескриптивная модель предполагает, что для разных ситуаций отток будет одинаковым:
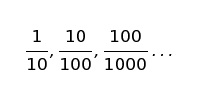
Проблема возникает при попытке составить прогноз на будущее, основываясь на показателях предыдущих периодов. Мы говорим: «Ожидается отток N% клиентов в следующем месяце, т.к. мы потеряли n% в этом. Рассчитать потери клиентов в данном случае поможет выборочная функция распределения:

В приведенном уравнении отток — выборка из бета-распределения. Подобная модель расчета используется с целью составить прогноз на основе имеющихся данных. Среднее значение распределения — это наиболее вероятная величина показателя.
При этом существует ряд других значений оттока, наблюдаемых лишь благодаря случайности. Бета-распределение показывает, насколько вероятно осуществление этих альтернатив — оно напрямую зависит от площади под кривой. Несмотря на то, что варианты 1/10 и 100/1000 дают одинаковый показатель оттока — 10%, они представляют абсолютно разные распределения. Ниже изображены варианты с 1/10, 10/100 и 100/1000 уровнями оттока, визуализированные как распределения:
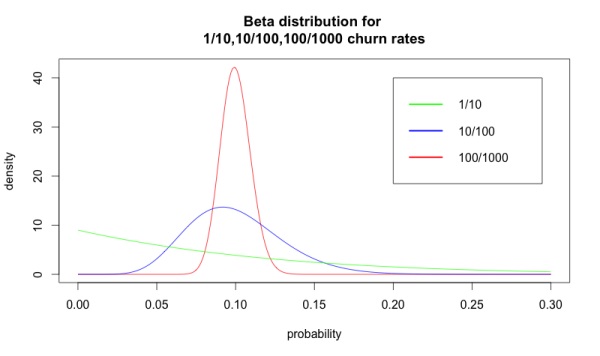
Ситуация подобна анализу результатов сплит-тестирования. Если вы рассчитали уровень оттока, в первую очередь следует проверить, является ли количество обработанных данных достаточным для того, чтобы утверждать о достоверности этого значения.
В качестве примера: если всего у вас 100 клиентов, в прошлом месяце вы потеряли 3% из них, а в этом — 6%, то вполне вероятно, что показатель churn фактически был одинаковым за оба периода. Выборочная функция распределения показывает, насколько полученная величина оттока соответствует данным, которые мы собрали.
Когда у нас нет достаточного количества данных, полученных в ходе сплит-тестирования, мы продолжаем его до тех пор, пока не достигнем нужной статистической значимости. Можно ли применить такой прием при определении значения оттока?
Одна из основных задач аналитика — рассчитывать churn каждый месяц. Рассчитывая отток за январь, мы не можем использовать данные февраля. Необходим способ, который смоделирует:
- Потери, которые мы наблюдали с помощью бета-распределения (фактический уровень оттока);
- Скорость оттока как плавающую величину.
Еще одна сложность заключается в том, что число клиентов, покинувших нас за месяц, в какой-то мере случайно. Если бы мы могли спрогнозировать его на 100%, модель оттока можно было бы свести к простейшей формуле.
Моделирование оттока
Сделаем шаг назад и попробуем создать модель, в которой можно не бояться недостаточного количества данных. Вместо того, чтобы фокусироваться на оттоке в изоляции, давайте рассмотрим клиентскую базу компании. Начнем с упрощенной модели, постепенно добавляя вышеупомянутые сложности.
На начальном этапе у нас есть переменные:
p0 — начальная численность потребительского населения, изменяющаяся под действием переменных;
с — коэффициент оттока;
a — новые покупатели;
l — потерянные клиенты (на основании начальной численности населения и уровня оттока).
Формула, определяющая число покупателей в данном месяце (p1), выглядит следующим образом:
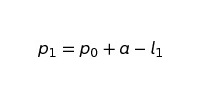
где
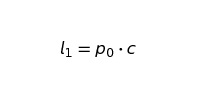
Теперь посмотрим, что происходит с течением времени, при условии что:
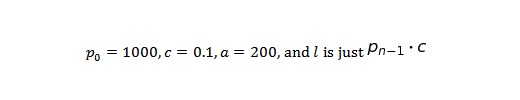
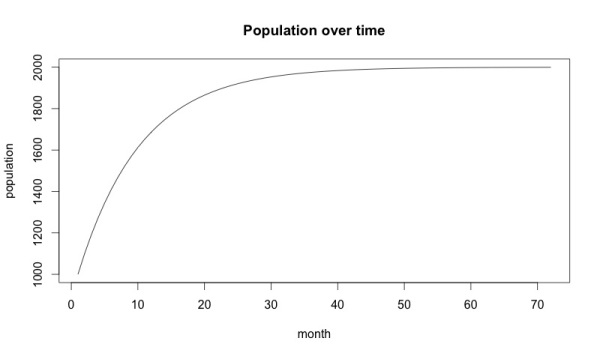
Первая проверка любой математической модели состоит в том, чтобы сопоставить ее с вашим мировоззрением. Рост, продемонстрированный на графике, гораздо более «гладкий», чем в реальном мире. К тому же, на 50-м месяце рост останавливается.
Все потому, что данная модель использует постоянное значение оттока (с) и новых покупателей (а). В действительности, ни то, ни другое не является постоянным. Модель нужно дорабатывать.
Вместо того чтобы учитывать постоянный c, начнем применять последовательность cn и an.
Создадим 12-месячную последовательность уровня оттока:
c = 0.1, 0.11, 0.1, 0.09, 0.085, 0.07, 0.073, 0.072, 0.07, 0.069, 0.07, 0.069
Также создадим последовательность из количества новых покупателей:
a = 200, 180, 210, 212, 230, 250, 240, 230, 245, 250, 255, 260
Эти последовательности моделируют год, в течение которого отток снижался, а число новых покупателей увеличивалось.
Формула для вычисления pn, изменится:
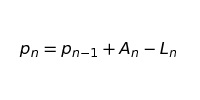
где:
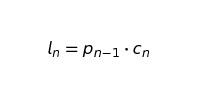
Помните, что p0 — «отправная» численность клиентов. Р1 — численность в конце января и т. д.
Диаграмма видоизменилась и стала выглядеть следующим образом:
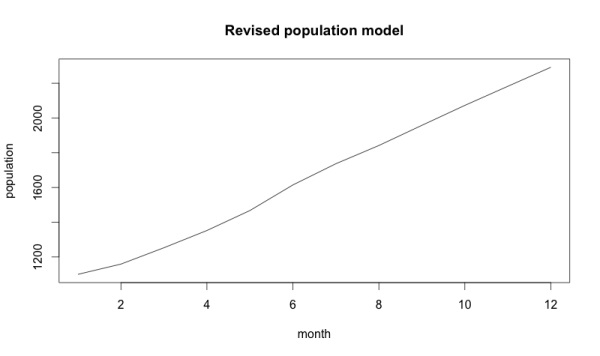
Невооруженным глазом видно, что это был хороший год!
Возникает другая проблема. Существует множество неопределенностей, которые не отражены в модели. Попробуем добавить в наш расчет небольшую долю вероятности.
Внимание на стохастические процессы!
Термин «стохастический» в математике означает «случайный». Т.е. итог такого процесса не может быть спрогнозирован в начальном состоянии системы. Наиболее известным стохастическим процессом является броуновское движение. Если вы почитаете о нем в Википедии, то столкнетесь с несколькими ужасающими уравнениями. Тем не менее, их идея достаточно проста.
Начнем с нормального распределения, которое определяется величиной µ - математического ожидания и σ — среднеквадратического отклонения.
Стандартным нормальным распределением называется распределение с µ=0 и σ=1. На графике оно выглядит следующим образом:
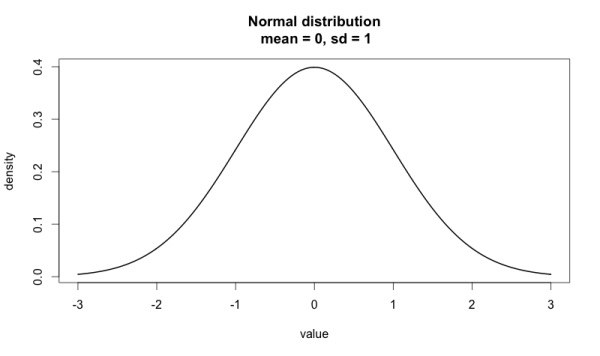
Выборка из нормального распределения — совокупность случайных чисел этой модели. Причем чем ближе число к середине, тем вероятнее его выпадение.
Если мы выберем 1000 случайных чисел из стандартного распределения N (0,1), то получим следующий график:
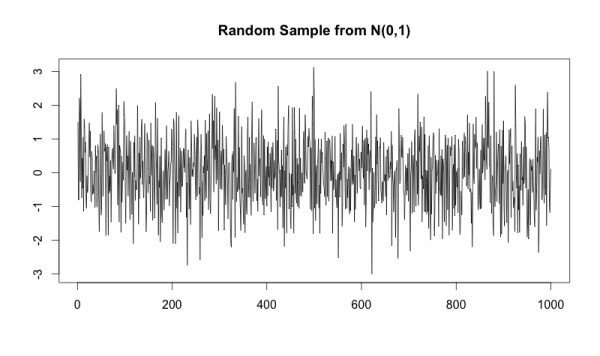
Для того чтобы привести образец к виду Броуновского движения, необходимо рассчитать нарастающий итог, когда каждая точка будет являться суммой всех предыдущих в модели.
Когда мы представим распределение в виде Броуновского движения, его график приобретет следующий вид:
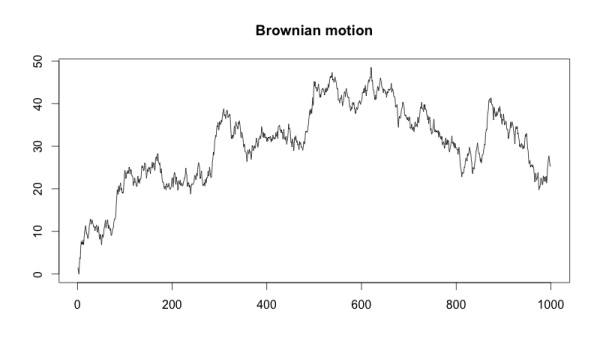
Если на первый взгляд график кажется беспорядочным, то после использования метода нарастающего итога он становится похож на схемы колебания курса акций! На самом деле, Броуновское движение является важным компонентом модели Блэка-Шоулза (Black-Scholes model), применяемой для ценообразования опционов. Кто знал, что прогнозирование оттока приведет нас в мир финансов!
Важно отметить: если среднее значение нормального распределения больше нуля, модель броуновского движения будет иметь тенденцию движения вверх. Если среднее значение меньше нуля — график устремится вниз. Такое движение называется дрейфом, т.к. случайный процесс дрейфует в определенном направлении.
Стохастическая модель оттока
Следующим этапом прогнозирования оттока является формулировка стохастического дифференциального уравнения. Классическое уравнение помогает описать переменную или функцию. Но наша разновидность будет отличаться. Стохастическое дифференциальное уравнение будет характеризовать случайный процесс!
Мы предполагаем, что отток и приток — случайные процессы, которые характеризуют динамику численности потребительского населения на протяжении долгих лет. Чтобы лучше понять процесс, отдельно рассмотрим приток — как компонент модели.
Определим приток как Броуновское движение с математическим ожиданием µacq и среднеквадратическим отклонением σacq.
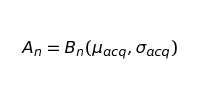
Формула показывает, что привлечение клиентов за период n — это n-ый шаг в Броуновском движении. Хитрость в понимании — n-ый шаг — не просто число, а пространство из множества вероятных значений.
Имитировать отток немного сложнее. За основу модели также возьмем Броуновское движение:
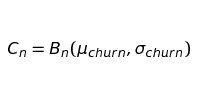
Данное уравнение — лишь теоретическое изменение оттока, которое в реальности мы никогда не сможем наблюдать. Чтобы точно представлять потери, необходим еще один шаг. Ведь отток — выборка бета-распределения со средней величиной cn:
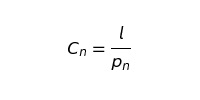
где l:
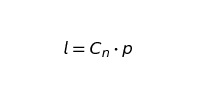
Теперь наша функция будет выглядеть как:
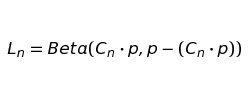
И в итоге получаем:
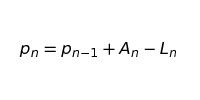
Полученное уравнение очень похоже на последнюю выведенную нами формулу. Ключевое отличие в том, что Аn и Ln — случайные процессы, а не фиксированные значения в последовательности.
Посмотрим, как будут выглядеть результаты выборки в данном случае. Все, что нужно — определить значения некоторых параметров.
µchurn = 0.001, σchurn = 0.001
µacq = 0.05, σacq = 40
p0 = 1000
Предполагаем, что исходное значение оттока 0,1, а приток равен 200 (т.е. уровень оттока в начале 10%, а за период мы получаем 200 клиентов). На рисунке ниже графическое изображение стохастического процесса на период 72 месяца.
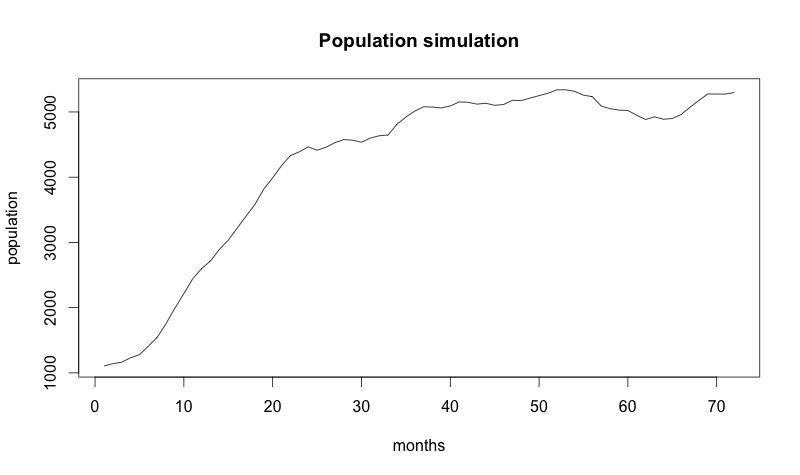
Не забывайте — стохастическая модель предполагает, что каждый раз, когда мы запускаем ее, мы получаем разные ответы!
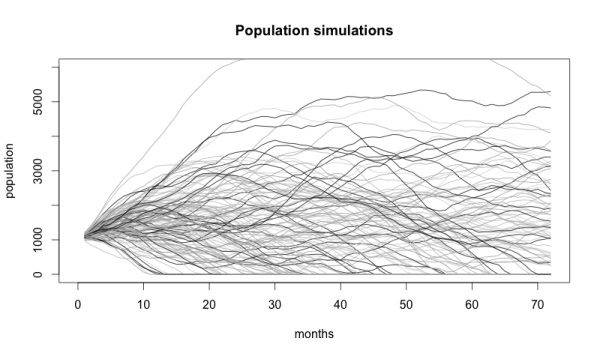
Вы можете сказать: «В моей компании ничего не бывает случайно! Мы не просто так занимаемся планированием!» Стохастические модели не утверждают, что события случайны. Они лишь полагают, что события не определены.
Например, каждый раз, когда вы проводите сплит-тестирование, существует шанс, что ваше решение неправильно. Даже если результат будет определен с 99,99% точностью, остается возможность ошибки. Предположим, резко изменился источник трафика… Или ваша система сбора статистики дала сбой.
Незначительные колебания происходят чаще, чем крупные, и нормальное распределение учитывает это. Кроме того, нормальное распределение предполагает, что вы постоянно работаете над улучшением продукта, а команда маркетологов регулярно повышает конверсию (об этом говорит дрейф процесса).
Моделирование данных, полученных наблюдением
Нашей стохастической модели по-прежнему не хватает параметров μchurn, σchurn, μacq, σacq. Помните, за μ мы принимаем общую тенденцию оттока и приобретения клиентов, за σ — количество неопределенностей, с которыми мы сталкиваемся.
Будем использовать предыдущие значения оттока и притока клиентов:
с = 0.1, 0.11, 0.09, 0.085, 0.07, 0.073, 0.072, 0.07, 0.069, 0.07, 0.069
a = 200, 180, 210, 212, 230, 250, 240, 230, 245, 250, 255, 260
Теперь рассчитываем μ и σ на основании собранных статистических данных. Наша модель предполагает накопительный итог значений нормального распределения. При этом нельзя просто взять математическое ожидание и отклонение от него. Мы должны рассчитать разницу между каждой стадией:
cdiff = 0.010, -0.010, -0.010, -0.005, -0.015, 0.003, -0.001, -0.002, -0.001, 0.001, -0.001
adiff = -20, 30, 2, 18, 20, -10, -10, 15, 5, 5, 5
Затем, используя приведенные ниже формулы, находим μ и σ:
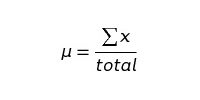
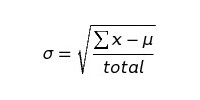
Получаем:
μchurn = -0.002818182
σchurn = 0.006925578
μacq = 5.454545
μacq = 5.454545
С помощью параметров, полученных эмпирическим путем, строим стохастическую модель:
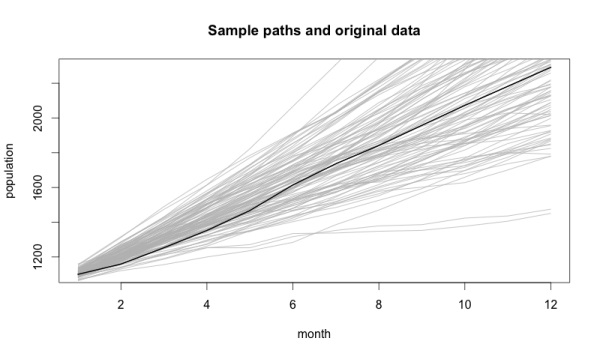
Самая яркая линия на графике — данные, на которых основана полученная модель. Факт, что исходная информация находится в центре — хорошая проверка объективности нашей модели. Остальные варианты, отмеченные светлыми линиями — вероятные пути развития событий.
Еще одно доказательство правильности полученной модели: чем дальше мы продвигаемся вперед во времени, тем шире становится диапазон возможных вариантов. Ведь чем дальше мы прогнозируем, тем менее уверены в своих словах.
Использование метода на практике
Руководители обычно не хотят, чтобы вы показали им стохастический процесс со словами: «Посмотрите, как много мы не знаем! Удивительно, не правда ли?» Мы описали, насколько сложно прогнозировать уровень оттока, но как применить модель на практике?
Анализируя данные за предыдущий период, вы можете построить модель сегодняшнего дня и посмотреть, по какому именно пути стали развиваться события. Если ваша компания не намечает глобальных перемен, то, скорее всего, дальше процесс будет протекать по аналогичной схеме.
Анализируя информацию предыдущих периодов, вы можете попытаться разобраться в будущем. Используя данные за 12 месяцев, вы видите, что модель предсказывает на следующие 6:
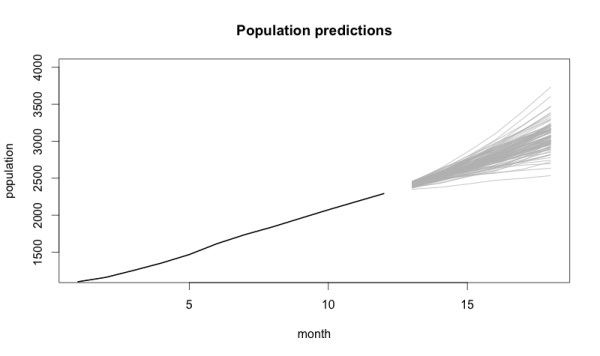
Если генеральный директор видит в воображении расширение клиентской базы до 4000 человек за полгода, стохастическая модель поможет вам с научной точки зрения объяснить, что это невозможно даже с учетом лучшего исхода событий. В случае «снижения» цели до 2500 клиентов модель подскажет, какие изменения стоит внести в работу.
Заключение
Прогнозировать отток достаточно трудно — всегда остается некоторая неопределенность. Однако, она не сможет изменить статус оттока как важнейшей SaaS-метрики.
Рассчитывая данный показатель любым способом, убедитесь, что вы понимаете свои ограничения. Чем меньше у компании клиентов, тем выше точность расчета. Чем больше клиентов — тем больше вероятность вмешательства в процесс «сторонних» сил, и, как следствие, ниже точность прогноза.
Высоких вам конверсий!
По материалам: blog.kissmetrics.com, image source: Rehman Asad