При всех восторженных разговорах о том, как чудесны (и насколько они огромны, не забудьте упомянуть об этом!) большие данные (Big data), один из самых любимых маркетологами инструментов оптимизации конверсии (CRO) — сплит-тестирование — работает явно с малыми данными (small data). Сама же по себе оптимизация, удачная или нет, определяется множеством факторов, но в конце концов сплит-тестирование в действительности сводится только к исследованию статистической выборки.
Предположим, что вы показываете 2 альтернативные версии надписи на CTA-кнопке (например, «Скидка 50%» против «Получите два по цене одного») посетителям вашего лендинга. Вы смотрите, насколько хорошо работает каждый вариант, а затем принимаете решение, какой из них оставить на посадочной странице для получения максимальной отдачи.
Если судить по описаниям, то сплит-тест представляет собой достаточно несложный процесс. В некотором смысле так и есть. Сложности появляются тогда, когда возникают вопросы относительно статистической значимости проведенного тестирования, в частности, о том, что такое P-значение (P-value) и как его можно интерпретировать для того, чтобы уверенно принимать обоснованные бизнес-решения.
Чтобы начать разбираться в этих на самом деле глубоких вопросах, нужно иметь базовое представление о том, что такое выборка данных (sampling, сэмплинг).
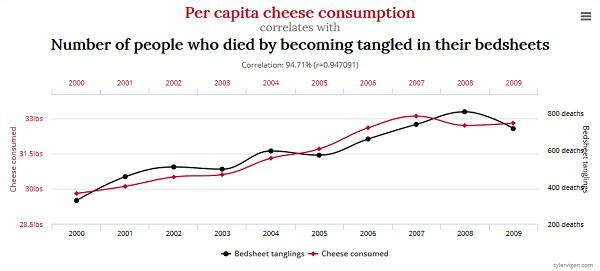
«Сыр без молока не сделать»
Мэтт Гершофф (Matt Gershoff), эксперт по оптимизации конверсии с более чем 15-летним опытом, так объясняет важность выборки:
«У меня в колледже был профессор математики, который взлетал как баллистическая ракета, когда кто-нибудь в классе допускал ошибку, связанную с базовыми концепциями его науки. Должно быть, он вырос на ферме, так как его остроты имели некий "сельскохозяйственный оттенок".
Его любимым присловьем было: "Как вы можете сделать сыр, если вы не знаете, где взять молоко?".
При этом профессор, вероятно, имел в виду, что нельзя эффективно воплощать идеи на практике, если не понимать их концептуальные основы. Для оптимизатора конверсии условным "сыром" станет сплит-тестирование, а выборка будет "молоком"».
Попробуем выяснить, где мы сможем найти наше «молоко».
Несколько предварительных пояснений
Для начала напомним, из каких базовых «строительных блоков» состоят A/B-тесты:
Среднее значение (Mean) — средняя величина (Average), среднее число конверсий; напомним, что для коэффициента конверсии (Conversion rates) это будет просто число событий n (конверсий), умноженное на вероятность (n*p).
Дисперсия случайной величины (Variance) — средняя вариабельность (изменчивость) данных. Основной смысл этого параметра: чем выше дисперсия, тем с меньшей точностью можно предсказать среднее значение для каждого отдельного члена статистической совокупности.
Распределение вероятности (Probability distribution) — это функция (для простоты можно думать о распределении как о правиле), определяющая вероятность некоего результата (исхода). Например, результат бросания игральной кости определяется равномерному распределению вероятности — все числа имеют один шанс из 6 оказаться на верхней грани кубика (вероятность p = 1 / 6).
В дальнейших рассуждениях о выборке мы будем в основном использовать нормальное распределение, графически отображающееся в виде колоколообразной кривой. Помните, что распределение вероятности в совокупности равняется 1 (100%).
Статистический критерий как еще один ключевой показатель эффективности
Статистический критерий (Test statistic) — это показатель, используемый при проведении сплит-тестов для сравнения результатов, полученных при испытании варианта А и варианта B образца (например, разных заголовков лендинга; вариантов может быть больше двух). Статистический критерий проще всего воспринимать как еще один из ключевых показателей эффективности (KPI, Key Performance Indicator).
Если этот KPI нашего сплит-теста близок к нулю, то у нас нет особых оснований полагать, что наши 2 варианта действительно отличаются.
Но чем дальше от нуля данный показатель, тем у нас больше доказательств, что эти 2 версии различаются по коэффициенту конверсии.
Новый KPI учитывает разницу между средними значениями (Mean) конверсии тестируемых вариантов и включает в себя вариабельность результатов испытаний.
Статистический критерий вычисляется по следующей формуле:
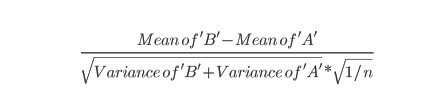
где Mean of 'A' и Mean of 'B' — среднее значение конверсии для вариантов А и В, Variance of 'A' и Variance of 'B' — дисперсия случайной величины для тестирования варианта А и для тестирования варианта B, n — совокупное число конверсий.
Пока этот показатель кажется сложным, не стоит слишком зацикливаться на математике: все сводится к определению разности между A и B — как разницы при обычном сравнении двух объектов — и делению полученной разности на вычисленную вариабельность данных.
Чем выше показатель вариабельности в знаменателе нашей дроби, тем большую ценность для устранения всякой неопределенности приобретает разность, наблюдаемая в числителе: даже если она довольно велика, большая вариабельность нивелирует ее и наш статистический критерий по-прежнему будет близок к нулю.
Получается, что чем выше дисперсия случайной величины, тем больше должна быть наблюдаемая разница показателей, чтобы мы могли получить высокое значение KPI нашего теста.
Помните, что чем выше значение статистического критерия, тем больше у вас реальных доказательств, что отличие в показателях конверсии не вызвано некой случайностью.
Сначала определяем выборку
Теперь отклонимся от предыдущей темы нашего повествования и уделим немного внимания выборке, что в дальнейшем позволит нам пролить свет на таинственное P-значение.
Для наглядности предположим, что мы устраиваем и пытаемся прорекламировать конференцию по вопросам веб-аналитики и оптимизации конверсии. Так как наше мероприятие будет иметь успех только тогда, когда нас посетит хотя бы некоторый необходимый минимум участников, мы хотим мотивировать их на предварительную регистрацию. Ранее мы использовали промокод «Analytics200» для получения 200-долларовой скидки на право участия в конференции. Но с учетом того, что сплит-тестирование — это актуальная, «горячая» тема, может ли быть так, что альтернативный промокод «A/BTesting200» поможет нам увеличить количество зарегистрировавшихся?
Следовательно, нам нужно провести сплит-тестирование контрольного («Analytics200») и альтернативного («A/BTesting200») промокодов.
Мы зачастую воспринимаем сплит-тест как один неразрывный процесс, хотя на самом деле его практическая «механика» делится на 2 части:
- Сбор данных (Data Collection) — та часть, когда мы показываем пользователям в качестве промокода либо «Analytics200», либо «A/BTesting200». Далее мы увидим, что здесь прослеживается некий компромисс между большей информированностью (меньшей вариабельностью) и расходами. Почему расходами? Потому, что мы вкладываем и время, и предшествующий потенциально лучший вариант в сплит-тест, надеясь, что мы найдем что-то лучшее, чем то, что у нас есть сейчас. Само по себе A/B-тестирование не является оптимизацией — это инвестиция в информацию.
- Анализ данных (Data Analysis) — вторая половина процесса тестирования, в которой мы выбираем метод получения вывода из «сырых» данных, собранных нами. Для большинства маркетологов, проводящих сплит-тестирование, это будет классический подход — проверка нулевой гипотезы. Вторая часть — это когда мы выбираем статистическую значимость (Statistical Significance), вычисляем р-значение и делаем выводы.
Тонкие различия между методами получения выводов кроются в различии фундаментальных предположений о случайности и статистике в целом. Если коротко, то английский статистик Рональд Эйлмер Фишер (Ronald Aylmer Fisher) использовал P-значение как доказательный критерий, позволяющий отвергнуть нулевую гипотезу (Null hypothesis); а Пирсон (Pearson) и Нейман (Neyman), например, для проверки статистических гипотез ввели в математическую статистику понятия ошибок первого рода и ошибок второго рода (Type 1 and Type 2 errors).
Поскольку в подходе Фишера к тестированию P-значения играют решающую роль, то мы будем пользоваться его методикой.
Косвенная логика статистического тестирования
Предоставим Мэтту Гершоффу возможность на простом примере объяснить нам одну из важнейших характеристик статистической значимости:
«Однажды ночью Салли и Боб ждут Джима, пообещавшего подвезти их домой после работы. Если Боб возвращается домой с Джимом почти каждую ночь, то у Салли это будет в первый раз. Боб говорит Салли, что в среднем он дожидается Джима около 5 минут.
После примерно 15 минут ожидания Салли начинает подозревать, что Джим не приедет, чтобы подвезти их. Тогда Салли спрашивает Боба: “Ты сказал, что Джим появляется здесь через 5 минут ожидания в среднем. А ждать его 15 минут — это в порядке вещей?” Боб отвечает: “Не волнуйся, тут такое автомобильное движение, что для меня не редкость ждать так долго, как мы сейчас ждем, если не дольше. Согласно моему опыту такое случается примерно в 15% случаев, когда я поджидаю Джима”. Салли немного успокаивается.
Обратите внимание: Салли спросила только о том, как часто приходится ждать Джима столь долго. После того, как она узнала, что наблюдаемое ею время ожидания не является особой редкостью, она почувствовала себя более комфортно, будто бы Джим уже показался на горизонте.
Интересно, что на самом деле она хотела знать, насколько велика вероятность того, что Джим подвезет их. Но этого она не узнала. Скорее, она лишь получила сведения о том, какова вероятность — с учетом всех поездок Боба с Джимом — появления водителя на 15 минут позже.
В этой косвенной логике и заключается суть классической статистической проверки гипотезы».
Вернемся к нашей гипотетической конференции
Ради аргументации наших последующих рассуждений предположим, что реклама конференции через промокод «Analytics200» имеет истинный коэффициент конверсии 0,1 (10%). В реальном мире этот показатель скрыт от нас — вот почему мы в первую очередь уделяем внимание выборке — но в нашем моделировании сплит-теста мы точно знаем, что конверсия равна 0,1. Значит, каждый раз, когда мы посылаем промокод «Analytics200», примерно 10% получателей рассылки регистрируются на конференцию.
Итак, отправив 50 потенциальным посетителям нашей конференции промокод «Analytics200», мы ожидаем получить примерно 5 лидов. Однако мы не будем удивлены, что в действительности подписчиков окажется несколько меньше или несколько больше. Но что значит «несколько»? Будем ли мы удивлены, увидев цифру 4? А как насчет 10? 25 или вообще нуля?
А знаете ли вы, что P-значение может ответить на вопрос, насколько неожиданным будет этот результат?
Разовьем эту идею: возьмем не одну группу из 50 потенциальных лидов, а 1000 отдельных выборок по 50 человек в каждой (в общей сложности 5000 участников). После запуска симуляции сплит-теста и ее графического отображения получим гистограмму, расположенную ниже:
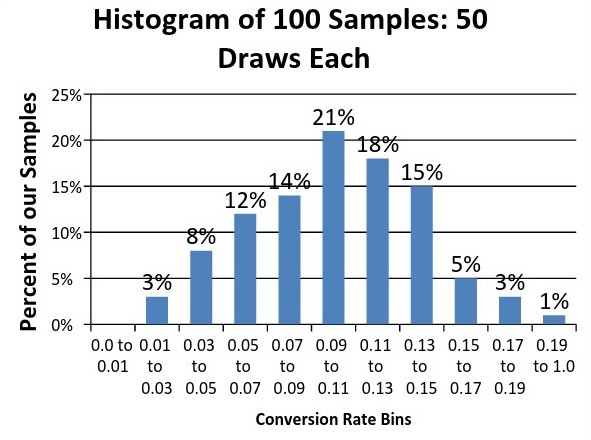
По горизонтальной оси расположены сгруппированные по частоте повторяемости коэффициенты конверсии (Conversion Rate Bins), по вертикальной — процентное соотношение выборок
Результаты нашего моделирования показали нам Conversion rates, расположенные в диапазоне 2% до 20%, а средний коэффициент конверсии 100 выборок составил 10,1%, что удивительно близко к его истинному значению.
Удивительные факты о выборках
Факт 1
Среднее значение конверсии повторяющихся выборок будет равно среднему коэффициенту преобразования для генеральной совокупности, из которой были взяты выборки.
Факт 2
Коэффициенты конверсии выборок будут приблизительно соответствовать нормальному распределению (Normal distribution; распределение Гаусса) — это означает, что большая часть выборок дает результаты преобразования, группирующиеся возле среднего значения конверсии, а случаи резких отклонений от среднего значения будут встречаться очень редко. Следовательно, мы можем использовать свойства нормального распределения (распределение Стьюдента, или t-распределение), чтобы узнать, насколько неожиданными будут полученные нами результаты сплит-тестирования.
Это важное умозаключение, потому что даже если коэффициент преобразования каждой отдельной выборки не соответствует истинной конверсии, то, вероятнее всего, он ближе к этому значению, чем нет. Моделирование теста показало, что 53% выборок имеет конверсию от 7 до 13%. Такой разброс результатов называется ошибкой выборки (Sampling error).
Осталось определиться с размерами выборки. Есть 2 параметра, определяющих доброкачественность выборки, т. е. сколько ошибок выборки мы получим:
1. Естественная вариабельность нашей генеральной совокупности.
2. Размер выборок.
Мы не имеем никакого контроля над изменчивостью генеральной совокупности, но мы можем управлять размером выборки. За счет его увеличения мы уменьшаем ошибку выборки, следовательно, мы будем более уверенны, что конверсия нашей выборки приблизится к истинному среднему значению.
Факт 3
Разброс результатов тестирования выборок уменьшается по мере увеличения объема выборочной совокупности (N). Чем больше размер выборки, тем точнее результаты теста каждой из них соответствуют истинному среднему значению.
Если мы подготовим еще один набор выборок для моделирования теста, но на этот раз увеличим размер выборочной совокупности с 50 до 200 человек, то разброс измеренных конверсий снизится до диапазона значений от 5% до 16,5% против предыдущего — от 2% до 20%. Обратите внимание, что промежутку коэффициентов конверсии от 7% до 13% будут соответствовать 84% выборок, тогда как в случае совокупной выборки, насчитывавшей 50 потенциальных лидов, этот показатель равнялся 53%.
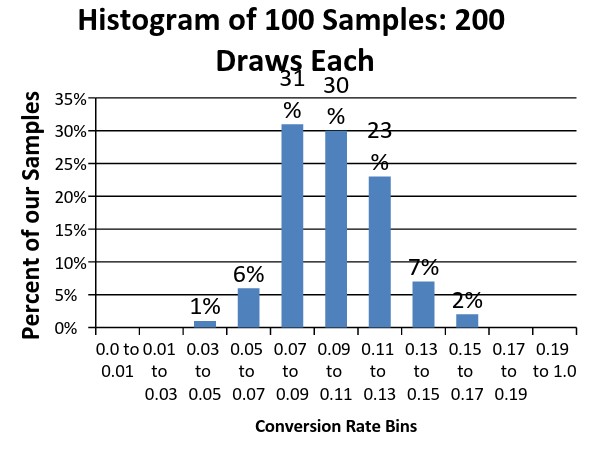
Гистограмма для 100 выборок по 200 человек в каждой
Мы можем считать размер выборки своего рода «регулятором», манипулируя которым мы уменьшаем или увеличиваем точность наших оценок. Увеличивая количество составляющих наших выборок до бесконечности, мы получаем идеально гладкие кривые нормального распределения. В условном «центре» каждой из них будет находится истинное среднее значение, а ширина кривой (дисперсия) будет распределяться размером каждой выборки.
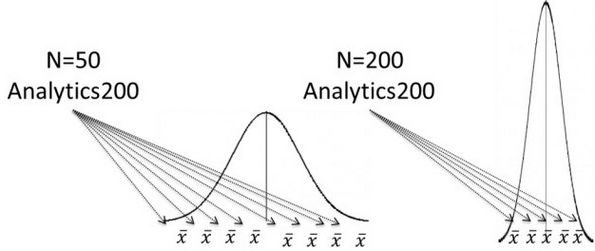
На левом графике значения, вероятнее всего, расположены далеко от истинного среднего, на правом — ближе к истинному среднему.
Почему данные не всегда должны быть большими
Даже если экономика с чисто академической точки зрения не является настоящей наукой, она тоже внесла свой вклад в сокровищницу знаний человечества. Например, вот это правило: при прочих равных условиях мы должны ожидать, что каждое наше последующее вложение будет приносить меньший доход, чем предыдущее. Этот принцип убывающей доходности вполне применим к процессу сплит-тестирования.
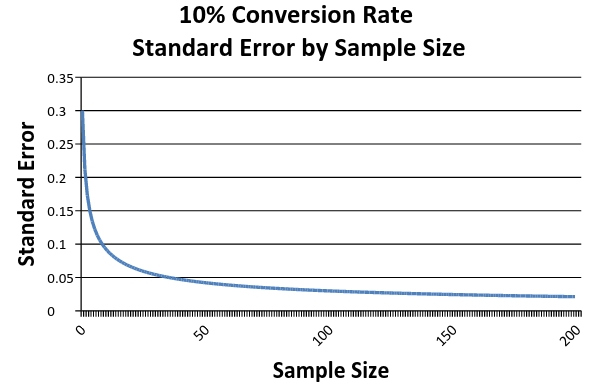
График зависимости величины стандартной ошибки выбора (Standard Error) от размера выборки (Samples Size)
На графике мы видим, что с увеличением размера выборочной совокупности ошибка выборки минимизируется. Однако снижается она с постоянно уменьшающейся скоростью, что означает, что мы получаем все меньше и меньше информации от каждого прибавления составляющих в нашей выборке.
Таким образом получается, что в данном конкретном случае переход к размеру выборки в 50 единиц резко уменьшает неопределенность, но следующее увеличение выборочной совокупности с 150 до 200 человек уже не дает столь заметного изменения. Иначе говоря, мы сталкиваемся с увеличением затрат на получение какой-либо дополнительной точности результатов. Это явление называется предельной величиной (Marginal value) данных, и его важно иметь в виду, когда речь заходит о тестировании. Именно в силу существования предельной величины более дорогостоящими и трудоемкими становятся сплит-тесты вариантов, имеющих очень близкие по значениям коэффициенты конверсии — труднее всего выбирать, основываясь на минимальных отличиях результатов.
Наш статистический критерий — как уже отмечалось ранее — учитывает величину разницы между результатами тестов для вариантов А и В, и то, насколько велика вариабельность (изменчивость) наших данных. Если наблюдаемая разница идет вверх, то статистический критерий увеличивается; снижаться он начинает при увеличении общей дисперсии.
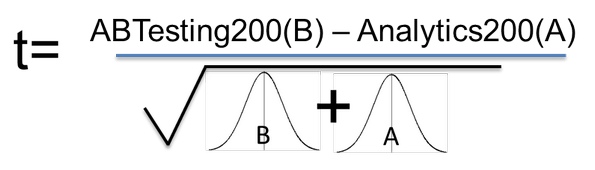
Формула определения статистического критерия (t) с подстановкой переменных для нашего гипотетического тестирования
С этого момента будем воспринимать наш статистический критерий строго по существу, не углубляясь в детали — так, как мы поступали, получая выборки для наших средних значений. Таким же образом как ранее на одиночное среднее значение мы теперь смотрим на разность 2 средних — B и A. Оказывается, что наши «3 удивительных факта о выборках» с таким же успехом применимы и к разностям средних значений.
А теперь, рассмотрев теоретические основы, мы наконец-то можем вплотную приступить к Р-значениям.
Контролировать, не впадая в нарциссизм
Вот как это работает. Мы собираем данные для обоих вариантов промокодов, «Analytics200» (А) и «A/BTesting200» (В). Затем мы делаем вид, что запускаем A/A-тест (не A/B!). Следовательно, мы смотрим на результат так, будто бы мы рассылали всей подписной базе один промокод «Analytics200».
Поскольку мы сами подбирали совокупности тестируемых образцов, мы знаем, что обе группы данных будут центрироваться возле одного и того же среднего значения, обладая одинаковой дисперсией — помните, что мы притворяемся, будто обе выборки взяты из одной генеральной совокупности (получатели промокода «Analytics200»). Так как нас интересует именно разница результатов, мы ожидаем, что разность средних значений (Analytics200 – Analytics200) будет равна нулю, так как конверсия одинаковой выборки должна иметь одно и то же значение.
Используя «3 факта о выборках», можно с достаточной степенью достоверности смоделировать гипотетический A/A-тест. Мы ожидаем, что в нашем случае в среднем никакой разницы в результатах между каждой выборкой не будет.
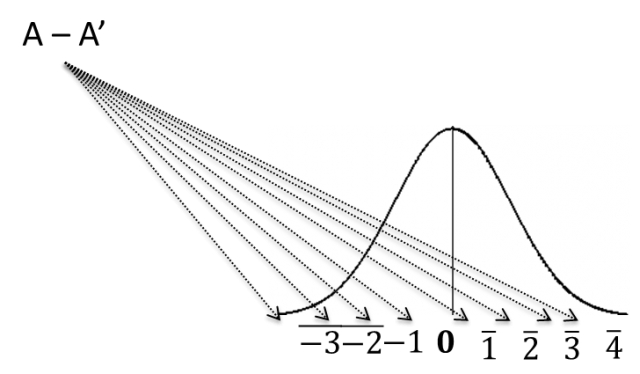
Вероятность получения значимых (отличных от нуля) результатов
Зная об ошибке выборки (Sampling error), мы не будем удивлены, увидев, что значения разности результатов будут близки к нулю, хотя и не равны ему. Но мы удивимся тому, что результат определяется тем, как далеко от нуля он расположен. Чтобы точно сказать, насколько вероятно появление результатов, отличных от нуля, нам достаточно принять как факт, что наши данные подчиняются нормальному распределению.
Значения, находящиеся далеко от нуля (например, 3 или –3), имеют низкую вероятность появления в результатах теста.
Наконец-то P-Value!
Заключительный шаг: смотрим, где наш статистический критерий уменьшается на данном распределении. Запустив A/A-тест, в диапазоне между – 2 и 2 мы не увидим ничего неожиданного. За пределами упомянутого диапазона мы обнаружим достаточно редко получаемые результаты.
Теперь наложим наш статистический критерий (t) на график распределения результатов A/A-теста. Так мы сможем увидеть, насколько далеко он находится от нуля, и какова вероятность получить такое значение в ходе A/A-теста.
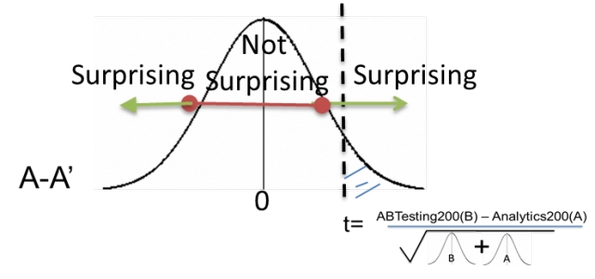
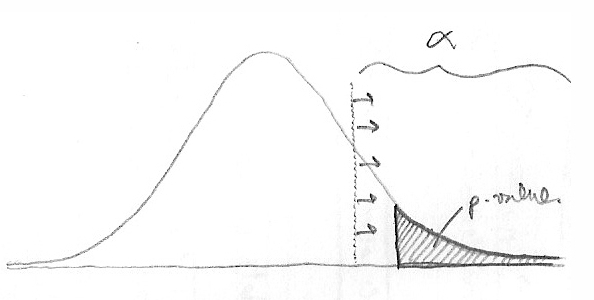
Статистический критерий (t) при наложении на кривую результатов A/A-теста может оказаться в «области ожидаемых результатов» (Not Surprising) или в «области неожиданных результатов» (Surprising)
Мы видим, что статистический критерий находится в «области неожиданностей». Вероятность появления «области неожиданности» определяется P-значением. Формально говоря, P-значение есть вероятность увидеть отличный от нуля (превосходящий) результат при предположении, что нулевая гипотеза верна.
Если наш тестовый критерий оказался в «области неожиданности», мы отвергаем нулевую гипотезу (как это было бы в случае настоящего A/A-теста). Если результат находится в «области ожидаемых результатов», мы принимаем гипотезу и проводим реальный сплит-тест.
Вместо заключения: 7 выводов
Вот что нужно помнить о P-значениях:
1. Тот, кто проводит тест, тот и определяет, что такое «неожиданность»
В реальности получается, что вывод из результатов теста зависит от того, кто выполняет данное исследование. То, как часто вы будете удивляться, зависит от того, насколько высоко P-значение, которое вы должны увидеть (или «уровень доверия» в методе Пирсона-Неймана; например, 95%), чтобы «удивиться».
2. Логика использования Р-значения весьма извилиста
Мы должны считать, что нулевая гипотеза верна, чтобы оценить доводы, с помощью которых мы можем отвергнуть нулевую гипотезу. Эта странная логика и является непрестанным источником путаницы.
3. Р-значение ничего не говорит нам о вероятности того, что вариант В лучше, чем А
Также мы не узнаем, сколь велика вероятность того, что мы ошиблись, предпочтя один вариант другому. Эти ошибочные представления чрезвычайно широко распространены, но тем не менее они остаются ложными.
Эту ошибку часто совершают даже так называемые «эксперты». Теперь вы сможете объяснить им, что P-значение есть лишь вероятность получения отличного от нуля результата в случае, если нулевая гипотеза верна.
4. В научном сообществе бурлят дебаты о значимости P-Value для извлечения выводов из сплит-тестов
Многие маркетологи отстаивают классическую проверку на статическую значимость как «золотой стандарт» отрасли, но среди специалистов по статистике по этому поводу не утихают споры.
5. Вы всегда можете получить высшее (существенное) P-значение
Помните, что стандартная ошибка с одной стороны зависит от изменений генеральной совокупности данных, с другой — от размера выборки. На изменения мы никак повлиять не можем, но ничто не мешает нам — если мы готовы «платить» за это — безостановочно собирать всё больше и больше данных.
На деле, однако, возникает вопрос: есть ли польза от полученных результатов? Сам по себе факт, что результат имеет высокое P-значение (или является статистически значимым в подходе Пирсона-Неймана), не имеет никакого практического значения.
6. Не волнуйтесь без повода
Самое главное — сперва собрать данные, на основе которых можно выработать работающую идею. Выбор между вариантами, очень мало различающимися меж собой, всегда труден. Если трудно выбрать «победителя», потому что предпочтение одного варианта другому приводит к похожему результату, то просто выберите один из вариантов и прекратите беспокоиться о том, правильно или неправильно вы поступили. Воспринимайте вашу программу тестирования как портфельные инвестиции: вместо покупки пакета ценных бумаг вы запускаете «пакет» сплит-тестов, ожидая получить от него дополнительную информацию, способную дать вам максимальную отдачу (повышение конверсии).
7. P-значение не равнозначно «правилу "Стоп"»
Это еще одна частая ошибка. Для того, чтобы получить достоверные результаты, позволяющие интерпретировать P-значение, вы определяетесь с размером выборки, а затем проводите тестирование. А вот дальше нужно выбрать время прекращения тестов, причем оно должно быть связано не с достижением высокого P-значения или статистической значимости, а с получением реальных результатов: оптимизации конверсии, роста выручки и т. д.
Высоких вам конверсий!
По материалам conversionxl.com, image source fickleandfreckled