Легендарный математик Карл Фридрих Гаусс (Carl Friedrich Gauss), изобретший метод статистической регрессии, недооценивал свое открытие. Он полагал, что не первый использует его, и был убежден в очевидности подхода. Гаусс публично заявил о своей находке лишь много лет спустя, когда его современник Адриен Мари Лежандр (Andrien-Marie Legendre) независимо от него открыл и опубликовал аналогичный метод.
Заявление Гаусса о том, что он обнаружил статистическую регрессию до Лежандра, спровоцировало один из самых известных споров в истории науки. Не без борьбы, но все же Гауссу удалось доказать свое право считаться первооткрывателем. Сегодня когда-то казавшееся своему автору незначительным открытие лежит в основе современной статистики и науки о данных.
Что такое статистическая регрессия?
Выражаясь простым языком, регрессия — это инструмент, предназначенный для исследования взаимосвязи между переменными. Он часто используется для прогнозирования будущего, и понимания, какие факторы влияют на результат.
Например, если вы хотите выяснить, какую роль играет образование с точки зрения зарплаты, предположить, кто победит на следующих выборах, или спрогнозировать эффект нового препарата, у вас есть отличная возможность — применить регрессию в действии.
Историк статистики Стефан М. Стиглер (Stephen M. Stigler) называет регрессию «автомобилем» статистического анализа: «Несмотря на ограничения, случайные происшествия и несущественные погрешности, данный метод и его многочисленные вариации составляют основу статистического анализа, и в настоящее время известны и оценены почти все из них».
Однако почему когда-то столь очевидная для Гаусса регрессия приобретает определяющее значение в современной науке?

На рубеже XVIII и XIX веков совершенствование способов навигации в океане было, пожалуй, важнейшей научно-практической проблемой. Эпоха Великих географических открытий привела к значительному обогащению и прибыльной торговле, но морские путешествия по-прежнему оставались опасными и ненадежными. Совершенствование технологий в этой области требовало значительных денежных вложений. С более точной навигацией суда и грузы, которые они перевозят, достигали бы целей более эффективно.
Учитывая огромные экономические выгоды, связанные с улучшением навигации и геодезии, в моде были исследования по измерению земли. В это время ключевым инструментом геодезистов стало использование движений других планет и комет по отношению к Земле, как способа понять форму и свойства планеты. Благодаря этим исследованиям, поддерживаемым монархами и аристократами, были улучшены карты и знания о местности, что в свою очередь позволило найти первый быстрый и безопасный путь из Португалии в Индию.
В таком историческом контексте математики Карл Фридрих Гаусс и Адриен Мари Лежандр независимо друг от друга и открыли метод наименьших квадратов (least squares) — важнейший инструмент статистической регрессии.
Наименьшие квадраты — это способ использования данных для количественных прогнозов. Эти прогнозы оптимизированы таким образом, что для любой точки в наборе данных возможность умножения ошибки модели на саму себя (получение квадрата) сводится к минимуму. И Гаусс, и Лежандр использовали метод наименьших квадратов для изучения орбит комет на основе неточных измерений их предыдущего местоположения:
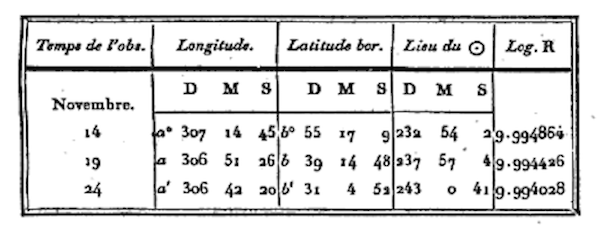
Набор данных, который использовал математик Андриен Мари Лежандр для демонстрации статистической регрессии, впервые опубликованной им в начале XIX века
Проблемы, которыми занимались Гаусс и Лежандр, довольно сложны для понимания, однако сам метод можно объяснить на относительно простом примере. Представьте, что вам предстоит вести урок у пятиклассников. Вам известны пол, рост и вес всех учеников. Вдруг вам таинственно сообщают, что один из учеников сегодня отсутствует, но незнакомец знает только пол и рост школьника, но не его вес. Как вычислить вес ученика?
Существуют различные виды критериев оптимизации (или признаков, по которым судят об оптимальности решения задачи), на которые вы могли бы опереться. Например, критерий, минимизирующий абсолютную погрешность вашей догадки, или тот, который имеет наименьший шанс отличаться больше, чем на 10 фунтов (приблизительно 4,5 кг). Метод наименьших квадратов хорош тем, что минимизирует квадратичную ошибку.
Но что такого особенного в этой квадратичной ошибке? Почему и Гаусс, и Лежандр независимо друг от друга обратили на нее внимание?
Есть две основные причины, по которым квадратичная ошибка была практически сразу принята математическим сообществом. Во-первых, в то время ее было сравнительно легко вычислить (сегодня в меньшей степени). Хотя существует простая формула, с помощью которой можно получить наилучшее предположение для минимизации квадратичной ошибки, вычислить лучшее предположение для любого другого критерия оптимизации, в том числе абсолютную погрешность — серьезное испытание.
Во-вторых, оценка на основе наименьших квадратов имеет некоторые отличные статистические свойства. При определенных условиях вы можете сделать предположение, что ваша ошибка нормально распределяется, что довольно удобно для понимания того, насколько вы можете быть уверены в своей догадке:
Надпись на картинке: слева — нормальное распределение, справа — паранормальное распределение. Автор шутки: Роберт Буксбаум (Robert Buxbaum)
Лежандр первым опубликовал метод наименьших квадратов. В своей работе под названием «Новый метод определения орбит комет» (1805 г.) ученый продемонстрировал оригинальную точку зрения и пример использования наименьшего квадрата регрессии. Лежандр был уверен, что является первооткрывателем метода:
«Из всех принципов, которые могут быть предложены для оценки образца, мы полагаем, что нет более подходящего, более точного и простого, чем метод, который мы использовали… суть метода — в минимизации суммы квадратов отклонений».
К сожалению для Лежандра, один из блестящих умов в истории науки уже работал над той же проблемой.
В чем заслуга Гаусса?

Карл Фредрих Гаусс был одним из величайших математиков в истории и своего рода двигателем науки — его изображение можно было встретить даже на немецких марках
Из-за удивительного вклада в развитие математики Карла Фредриха Гаусса иногда называют «королем математиков». И хотя Лежандр признавал гений Гаусса, не исключено, что в узком кругу он называл Гаусса менее добрыми именами. По академическим меркам Гаусс совершил непристойный поступок, украв заслугу открытия наименьшего квадрата регрессии прямо из-под носа у Лежандра.
В трактате Гаусса «Теория движения небесных тел, обращающихся вокруг Солнца по коническим сечениям» математику удалось решить, казалось бы, неразрешимую проблему расчета планетарных орбит. Главной особенностью теории Гаусса была ее способность предсказать, в какой точке ночного неба появится астероид Церера, чего не мог сделать ни один другой ученый того времени. Большое количество сложных математических и геометрических проблем удалось решить при помощи метода наименьших квадратов.
«Наш принцип, который мы используем с 1795 года, был недавно опубликован Лежандром…» — пишет Гаусс, — «который объясняет несколько иные свойства этого метода». Как и другие математики того времени, Гаусс употребляет королевское «мы».
Лежандр был потрясен. Решение Гаусса претендовать на открытие, опубликованное им ранее, конечно, выглядело сомнительно. Известный историк статистики Стивен Стиглер говорит, что решение Гаусса было «лишено сочувствия». Лежандр отправил Гауссу письмо, чтобы выразить свое разочарование:
«Не без удовольствия я обнаружил, что в своих исследованиях вы использовали тот же метод, который я назвал методом наименьших квадратов в своих наблюдениях за кометами… Признаюсь вам, что я придаю некоторое значение этому маленькому открытию. Поэтому я не буду скрывать от вас, сэр: я испытал некоторое сожаление, что вы, ссылаясь на мою работу, говорите, что обнаружили метод в 1795 году. Не существует открытия, которое нельзя было бы приписать себе, сказав, что те же вещи были найдены на несколько лет раньше; но если не дано этим словам доказательства, состоящего в указании места, где они опубликованы, то это утверждение становится беспредметным и представляет собой только обиду для истинного автора открытия».
Лежандр заканчивает письмо весьма неуважительно:
«У вас хватает собственных богатств и нет необходимости завидовать кому-то. Я совершенно уверен в своем открытии. Кроме того, у меня есть основания оспаривать ваше высказывание».
Гаусс никогда не отступал от своего заявления о том, что он открыл метод первым. Хотя это высказывание выглядело не вполне убедительно, все же преобладающее количество доказательств говорит в пользу Гаусса. Его коллеги подтвердили, что он объяснял им метод наименьших квадратов, и были соответствующие записи расчетов, которые, безусловно, не могли быть сделаны иным методом.
Гаусс не опубликовал свое открытие сразу, потому что предпочитал полностью развить свою идею, прежде чем обнародовать ее. Он руководствовался девизом: «Лучше меньше да лучше». Историк математики Эрик Темпл Белл (Eric Temple Bell) считает, что если бы все теории Гаусса были опубликованы тогда, когда они пришли к нему, в математике произошел бы скачок более, чем на 50 лет вперед.
Сегодня Гаусс считается изобретателем метода наименьших квадратов и регрессии, потому что он предложил более точное описание, чем Лежандр. Стиглер объясняет: «Когда Гаусс опубликовал метод наименьших квадратов, стало очевидно, что в своих исследованиях он продвинулся намного дальше Лежандра как в концептуальном, так и в техническом плане, связав метод вероятности и представив алгоритмы для расчета оценок».
При этом Гаусс не придавал особого значения методу наименьших квадратов, не считая его величайшим открытием. Однажды Фредрих написал коллеге, как он был удивлен, что никто из его предшественников не открыл этот метод ранее. И добавил, что не будет публиковать его, не желая minxit in patrios cineres, что в переводе с латинского означает «осквернять прах своих предков».
Тем не менее, Гаусса всю жизнь беспокоили сомнения людей в том, что именно он открыл регрессию. Р. Л. Плакетт (R.L. Plackett) писал о Гауссе: «Искренное принятие принципа приоритетнее, чем его публикация».
По мнению Стиглера, такого рода приоритетные разногласия характерны для истории научных открытий. И поясняет: «Спор о приоритете свидетельствует о том, что происходит нечто важное»
Хорошо, но причем здесь регрессия?

Будучи первооткрывателями основного свойства регрессии, ни Гаусс, ни Лежандр не употребляли слово «регрессия» относительно своего метода.
Термин был впервые применен к статистике энциклопедистом Фрэнсисом Гальтоном (Francis Galton). Гальтон внес существенный вклад в развитие статистики и генетики. К сожалению, его исследования наследственности также привели к изобретению термина «евгеника» и утверждению права на селекцию лучшего общества.
Гальтон использовал термин «регрессия», чтобы объяснять явления природы. В 1870 году он собрал данные о высоте потомков экстремально высоких и экстремально низких деревьев. Он хотел выяснить, как связаны деревья со своими предками. Ученый опубликовал результаты исследования в 1886 году под названием «Регрессия к среднему в наследственности».
«Из моих наблюдений следует, что потомство не стремится походить на родителей по размеру, но всегда получается более средним — ниже, чем предки, если предки были высокими, и выше, чем предки, если предки были низкими».
В наше время явление, обнаруженное Гальтоном, так и называется — регрессией к среднему. Так, если сегодня чрезвычайно жаркий день, можно ожидать, что завтра тоже будет жарко, но уже не так жарко, как сегодня. Если игрок в бейсбол только что завершил свой лучший сезон в карьере, скорее всего, в следующем году вы будете разочарованы его игрой. За экстремальными событиями следуют более нормальные.
Регрессия стала ассоциироваться с методом наименьших квадратов приблизительно в конце XVIII века. Карл Пирсон (Carl Pearson), один из основателей математической статистики и коллега Гальтона, заметил, что если отметить рост родителей на оси x и их детей на оси y — линия, наилучшим образом соединяющая данные в соответствии с методом, имеет наклон меньше единицы (y < x), что фактически является математическим представлением «регрессии к среднему». Пирсон называет этот наклон на графике «линией регрессии». Таким образом, метод наименьших квадратов и понятие регрессии стали своего рода синонимами:
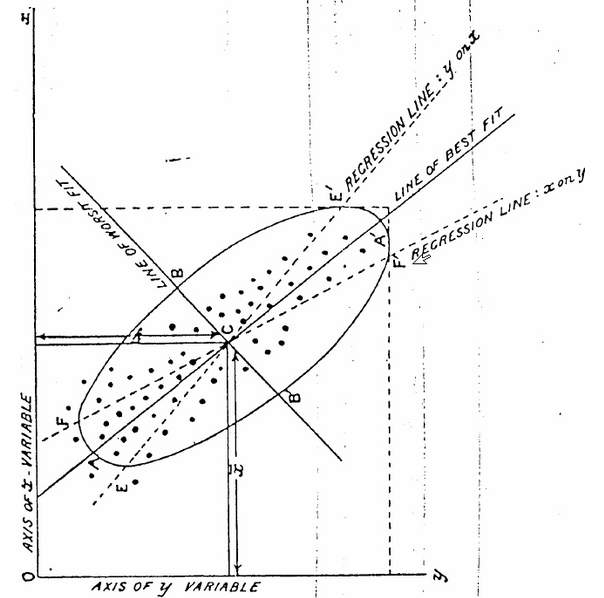
В 1901 году статистик Карл Пирсон использовал метод “линии регрессии” для расчета наименьших квадратов
Регрессионный анализ, каким мы его знаем сегодня, впервые был озвучен в работе одного из самых известных статистов XX века Р.А. Фишера. Ученый объединил труды Гаусса и Пирсона, чтобы разработать совершенную теорию оценки свойств наименьших квадратов. Благодаря работе Фишера, регрессионный анализ используется не только для прогнозирования и понимания корреляции, но и для того, чтобы сделать вывод (иногда неверный) о взаимосвязи между фактором и результатом. После Фишера появилось много важных расширений метода, в том числе логистическая регрессия, непараметрическая регрессия, регрессия Байеса и регрессия, включающая регуляризацию.
Развитие вычислительной техники сделало регрессию популярным методом. В 20-е годы XX века IBM создала автоматизированные табуляторы с перфокартами, которые можно было использовать для проведения сложных вычислений статистического анализа, таких как регрессия. До этого все расчеты делались вручную — регрессию можно было рассчитать для очень небольших наборов данных или тех, для которых приходилось производить в уме ряд вычислительных операций.
Вплоть до 1970-х годов вычисления для получения регрессии занимали несколько дней, и технология была доступна ограниченному числу исследователей. Только с появлением персонального компьютера использование регрессионного анализа стало массовым. Сегодня любой человек, имеющий персональный компьютер, может рассчитать регрессию для небольшого объема данных меньше, чем за секунду.
Гаусс и Лежандр удивились бы, узнав, что метод наименьших квадратов так популярен сегодня. Регрессионный анализ часто используется учеными, политическими аналитиками, журналистами и даже спортивными командам, чтобы предсказать будущее и понять прошлое. С развитием более сложных алгоритмов прогнозирования и формулирования выводов, старый добрый метод наименьших квадратов не утратил своей актуальности и по-прежнему остается жемчужиной статистического анализа.
Высоких вам конверсий!
По материалам: priceonomics.com, image source thcastor