Как вы думаете, что делает вашу «вторую половинку» особенной, значимой? Это связано с ее (его) личностью или с вашими чувствами, которые вы испытываете к этому человеку? А может, с простым фактом, что гипотеза о случайности вашей симпатии, как показывают исследования, имеет вероятность менее 5%? Если считать последнее утверждение достоверным, то успешных сайтов знакомств не существовало бы в принципе:
Мы все привыкли считать что-то значимое как нечто неповторимое, но статистика упрямо заявляет: это совершенно не так.
Когда вы проводите сплит-тестирование или любой другой анализ вашего сайта, неверное понимание «статистической значимости» может привести к неправильной интерпретации результатов и, следовательно, ошибочным действиям в процессе оптимизации конверсии. Это справедливо и для тысяч других статистических тестов, проводимых ежедневно в любой существующей отрасли.
Чтобы разобраться, что же такое «статистическая значимость», необходимо погрузиться в историю появления этого термина, познать его истинный смысл и понять, как это «новое» старое понимание поможет вам верно трактовать результаты своих исследований.
Немного истории
Хотя человечество использует статистику для решения тех или иных задач уже много веков, современное понимание статистической значимости, проверки гипотез, рандомизации и даже дизайна экспериментов (Design of Experiments (DOE) начало формироваться только в начале 20-го столетия и неразрывно связано с именем сэра Рональда Фишера (Sir Ronald Fisher, 1890-1962):

Рональд Фишер был эволюционным биологом и статистиком, который имел особую страсть к изучению эволюции и естественного отбора в животном и растительном мире. В течение своей прославленной карьеры он разработал и популяризировал множество полезных статистических инструментов, которыми мы пользуемся до сих пор.
Фишер использовал разработанные им методики, чтобы объяснить такие процессы в биологии, как доминирование, мутации и генетические отклонения. Те же инструменты мы можем применить сегодня для оптимизации и улучшения контента веб-ресурсов. Тот факт, что эти средства анализа могут быть задействованы для работы с предметами, которых на момент их создания даже не существовало, кажется довольно удивительным. Столь же удивительно, что раньше сложнейшие вычисления люди выполняли без калькуляторов или компьютеров.
Для описания результатов статистического эксперимента как имеющих высокую вероятность оказаться истиной Фишер использовал слово «значимость» (от англ. significance).
Также одной из наиболее интересных разработок Фишера можно назвать гипотезу «сексуального сына». Согласно этой теории, женщины отдают свое предпочтение неразборчивым в половых связях мужчинам (гулящим), потому что это позволит рожденным от этих мужчин сыновьям иметь такую же предрасположенность и произвести на свет больше своих отпрысков (обращаем внимание, что это всего лишь теория).
Но никто, даже гениальные ученые, не застрахованы от совершения ошибок. Огрехи Фишера досаждают специалистам и по сей день. Но помните слова Альберта Эйнштейна: «Кто никогда не ошибался, тот не создавал ничего нового».
Прежде чем перейти к следующему пункту, запомните: статистическая значимость — это ситуация, когда разница в результатах при проведении тестирования настолько велика, что эту разницу нельзя объяснить влиянием случайных факторов.
Какова ваша гипотеза?
Чтобы понять, что значит «статистическая значимость», сначала нужно разобраться с тем, что такое «проверка гипотез», поскольку два этих термина тесно переплетаются.
Гипотеза — это всего лишь теория. Как только вы разработаете какую-либо теорию, вам будет необходимо установить порядок сбора достаточного количества доказательств и, собственно, собрать эти доказательства. Существует два типа гипотез.

Яблоки или апельсины — что лучше?
Нулевая гипотеза
Как правило, именно в этом месте многие испытывают трудности. Нужно иметь в виду, что нулевая гипотеза — это не то, что нужно доказать, как, например, вы доказываете, что определенное изменение на сайте приведет к повышению конверсии, а наоборот. Нулевая гипотеза — это теория, которая гласит, что при внесении каких-либо изменений на сайт ничего не произойдет. И цель исследователя — опровергнуть эту теорию, а не доказать.
Если обратиться к опыту раскрытия преступлений, где следователи также строят гипотезы в отношении того, кто является преступником, нулевая гипотеза принимает вид так называемой презумпции невиновности, концепта, согласно которому обвиняемый считается невиновным до тех пор, пока его вина не будет доказана в суде.
Альтернативная гипотеза
Если нулевая гипотеза заключается в том, что два объекта равны в своих свойствах, а вы пытаетесь доказать, что один из них все же лучше (например, A лучше B), вам нужно отказаться от нулевой гипотезы в пользу альтернативной. Например, вы сравниваете между собой тот или иной инструмент для оптимизации конверсии. В нулевой гипотезе они оба оказывают на объект воздействия одинаковый эффект (или не оказывают никакого эффекта). В альтернативной — эффект от одного из них лучше.
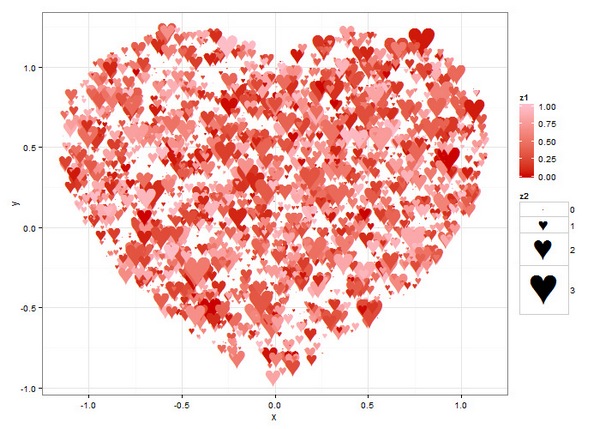
Ваша альтернативная гипотеза может содержать числовое значение, например, B – A > 20%. В таком случае нулевая гипотеза и альтернативная могут принять следующий вид:
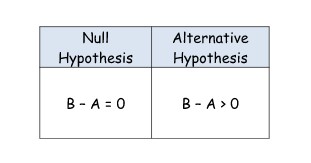
Другое название для альтернативной гипотезы — это исследовательская гипотеза, поскольку исследователь всегда заинтересован в доказательстве именно этой гипотезы.
Статистическая значимость и значение «p»
Вновь вернемся к Рональду Фишеру и его понятию о статистической значимости.
Теперь, когда у вас есть нулевая гипотеза и альтернативная, как вы можете доказать одно и опровергнуть другое?
Поскольку статистические данные по самой своей природе предполагают изучение определенной совокупности (выборки), вы никогда не можете быть на 100% уверены в полученных результатах. Наглядный пример: зачастую результаты выборов расходятся с результатами предварительных опросов и даже эксит-пулов.
Доктор Фишер хотел создать определитель (dividing line), который позволял бы понять, удался ли ваш эксперимент или нет. Так и появился индекс достоверности. Достоверность — это тот уровень, который мы принимаем для того, чтобы сказать, что мы считаем «значимым», а что нет. Если «p», индекс достоверности, равен 0,05 или меньше, то результаты достоверны.
Не волнуйтесь, в действительности все не так запутано, как кажется.
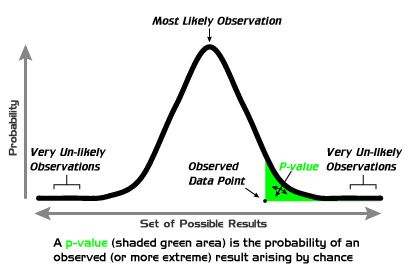
Распределение вероятностей Гаусса. По краям — менее вероятные значения переменной, в центре — наиболее вероятные. P-показатель (закрашенная зеленым область) — это вероятность наблюдаемого результата, возникающего случайно.
Нормальное распределение вероятностей (распределение Гаусса) — это представление всех возможных значений некой переменной на графике (на рисунке выше) и их частот. Если вы проведете свое исследование правильно, а затем расположите все полученные ответы на графике, вы получите именно такое распределение. Согласно нормальному распределению, вы получите большой процент похожих ответов, а оставшиеся варианты разместятся по краям графика (так называемые «хвосты»). Такое распределение величин часто встречается в природе, поэтому оно и носит название «нормального».
Используя уравнение на основе вашей выборки и результатов теста, вы можете вычислить то, что называется «тестовой статистикой», которая укажет, насколько отклонились полученные результаты. Она также подскажет, насколько близко вы к тому, чтобы нулевая гипотеза оказалась верной.
Чтобы не забивать свою голову, используйте онлайн-калькуляторы для вычисления статистической значимости:

Один из примеров таких калькуляторов
Буква «p» обозначает вероятность того, что нулевая гипотеза верна. Если число будет небольшим, это укажет на разницу между тестовыми группами, тогда как нулевая гипотеза будет заключаться в том, что они одинаковы. Графически это будет выглядеть так, что ваша тестовая статистика окажется ближе к одному из хвостов вашего колоколообразного распределения.
Доктор Фишер решил установить порог достоверности результатов на уровне p ≤ 0,05. Однако и это утверждение спорное, поскольку приводит к двум затруднениям:
1. Во-первых, тот факт, что вы доказали несостоятельность нулевой гипотезы, не означает, что вы доказали альтернативную гипотезу. Вся эта значимость всего лишь значит, что вы не можете доказать ни A, ни B.
2. Во-вторых, если p-показатель будет равен 0,049, это будет означать, что вероятность нулевой гипотезы составит 4,9%. Это может означать, что в одно и то же время результаты ваших тестов могут быть одновременно и достоверными, и ошибочными.
Вы можете использовать p-показатель, а можете отказаться от него, но тогда вам будет необходимо в каждом отдельном случае высчитывать вероятность осуществления нулевой гипотезы и решать, достаточно ли она большая, чтобы не вносить тех изменений, которые вы планировали и тестировали.
Наиболее распространенный сценарий проведения статистического теста сегодня — это установление порога значимости p ≤ 0,05 до запуска самого теста. Только не забудьте внимательно изучить p-значение при проверке результатов.
Ошибки 1 и 2
Прошло так много времени, что ошибки, которые могут возникнуть при использовании показателя статистической значимости, даже получили собственные имена.
Ошибка 1 (Type 1 Errors)
Как было упомянуто выше, p-значение, равное 0,05, означает: вероятность того, что нулевая гипотеза окажется верной, равняется 5%. Если вы откажетесь от нее, вы совершите ошибку под номером 1. Результаты говорят, что ваш новый веб-сайт повысил показатели конверсии, но существует 5%-ная вероятность, что это не так.
Ошибка 2 (Type 2 Errors)
Эта ошибка является противоположной ошибке 1: вы принимаете нулевую гипотезу, в то время как она является ложной. К примеру, результаты тестов говорят вам, что внесенные изменения в сайт не принесли никаких улучшений, тогда как изменения были. Как итог: вы упускаете возможность повысить свои показатели.
Такая ошибка распространена в тестах с недостаточным размером выборки, поэтому помните: чем больше выборка, тем достовернее результат.
Заключение
Пожалуй, ни один термин среди исследователей не пользуется такой популярностью, как статистическая значимость. Когда результаты тестов не признаются статистически значимыми, последствия бывают самые разные: от роста показателя конверсии до краха компании.
И раз уж маркетологи используют этот термин при оптимизации своих ресурсов, нужно знать, что же он означает на самом деле. Условия проведения тестов могут меняться, но размер выборки и критерий успеха важен всегда. Помните об этом.
Высоких вам конверсий!
По материалам blog.crazyegg.com