Традиционный подход к анализу тестов — так называемый t-тест, метод, применяемый в частотной статистике. Хотя он научно-обоснован, его недостаток: обращая внимание только на статистическую значимость, вы рискуете прибылью.
Сегодня обсудим, почему байесовский подход лучше частотных метрик. Звучит сложно, но не волнуйтесь — в конце поста вы сможете провести собственный байесовский анализ без особого труда.
Как создать успешную программу тестов?
Печальная правда в том, что многие стратегии тестирований умирают тихой смертью. Если не все члены команды верят в проект по оптимизации, вы потратите много времени, доказывая свою правоту. А вера в план тестов сильно зависит от числа удачных испытаний. Если ваш «коэффициент побед» очень низок — скажем, ниже 20%, — значит, сайт не меняется с течением времени, и энергия и мотивация людей быстро иссякает. Нет отдачи от усилий — нет увлеченности, не говоря уже о том, что желание финансировать проект быстро улетучивается без достаточного маркетингового ROI.
Без результатов вашу работу не заметят. Если одно из десяти испытаний «выстреливает», руководство сочтет тесты «балластом» — и понизит приоритет проекта, или вовсе закроет его.
Нужно больше побед!
Решение очевидно — нужно больше успешных тестов. Но сказать легко, а как сделать? Например, тестируя более смелые вариации — но есть и другой подход. Пересмотрите само восприятие «успешного» теста, изменив метод анализа.
Для оценки сплит-тестов принято использовать частотную статистику. Не поняли? Сейчас объясним.
Главная проблема частотных данных — результаты теста трудно интерпретировать. Так, t-тест (входящий в частотную статистику) проверяет, насколько отличаются значения двух независимых групп. Основное положение теста — нет никакой разницы между коэффициентами конверсии групп А и В. Это так называемая нулевая гипотеза.
С частотной обработкой результатов вы отвергаете эту гипотезу, желая доказать, что вариант В превосходит контрольную версию А. При заранее заданном уровне достоверности теста (как правило, 90% или 95%), вы оцениваете, ниже ли р-значение (1 — уровень достоверности) теста порогового р-значения. Если результат едва ли подпадает под нулевую гипотезу (скажем, р-значение — 0,02), то конверсия А отличается от В.
Поднимая «занавес тайны» над P-значениями, или Как научиться любить малые данные (Small Data)
Невиновен, пока не доказано обратное
Частотная статистика напоминает судебные процессы. Нулевая гипотеза в суде — ответчик не виновен. Это отправная точка: подсудимый не считается виновным, пока вина не доказана. Альтернативная гипотеза — виновность ответчика, которую еще предстоит доказать уликами.
Затем доказательства защиты и обвинения оцениваются. Судьи спрашивают себя: «Можно ли, с учетом имеющихся данных, считать ответчика невиновным?» Другими словами, актуальна ли нулевая гипотеза по-прежнему? Если она актуальна, мы не отвергаем ее, а утверждаем, что доказательств недостаточно для обвинительного приговора. В противном случае, мы отвергаем нулевую гипотезу.
Таким образом, t-тест основан на предположении, что варианты А и В равны. Это сбивает с толку, и не только вас: недавнее исследование показало, что более 80% маркетологов совершенно не понимают частотную статистику.
Последнее, что интересует маркетолога, это с какой вероятностью нулевая гипотеза ошибочна и версии теста не равны. Все, что он хочет знать — какая из версий эффективнее?
Иными словами, частотная статистика нерелевантна основному вопросу сплит-теста.
Победил или нет? Отличный вопрос!
Другая проблема — бинарность результатов. Вы либо выиграли, либо проиграли. Другими словами, вы либо отвергаете нулевую гипотезу, либо оставляете ее в силе. Места дискуссиям здесь нет.
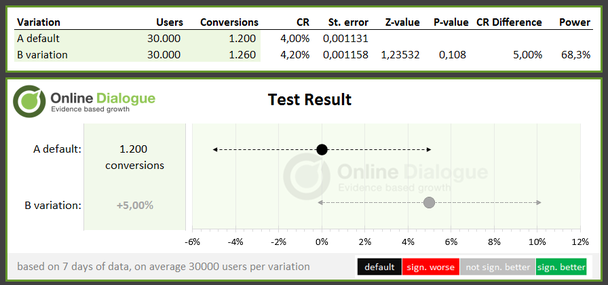
Взглянув на тест ниже, вы поймете, что победителя нет и вариацию не стоит реализовывать. Ведь р-значение недостаточно низкое, чтобы отвергнуть нулевую гипотезу. Поэтому тест неудачный, и маркетологи начинают сначала.
Но позитивные тенденции видны (рост конверсии — 5%). Просто улучшение недостаточно сильное, чтобы признать его заметным и значимым. Возможно, еще несколько конверсий, или чуть большая выборка, и результат стал бы другим.
Проще говоря — идея теста хороша, а гипотеза верна. Просто стоило провести испытание немного иначе или дольше. Но частотное тестирование — это поиск абсолютных победителей. Альтернативная гипотеза должна быть доказана так же достоверно, как преступление в суде — малейшие сомнения недопустимы. Нужно минимизировать риски, насколько это возможно.
Кстати, это неудивительно, если знать, что t-тестами проверяют лечебные препараты. Вряд ли фармацевтическая компания станет выводить на рынок лекарство без абсолютной уверенности в его пользе и безопасности.
Но интернет-маркетинг — не ядерная физика и не медицина. От маленького просчета тестировщика никто не пострадает. Жесткий упор на безопасность не способствует росту бизнеса. Чтобы выиграть, нужно рисковать — хотя бы немного.
Как запустить сплит-тест, который сделает ваш онлайн-бизнес по-настоящему успешным
Какова альтернатива?
Байесовский подход к оценке сплит-тестов в последние годы становится популярнее. Большинство известных программных решений для тестов обратились к байесовской оценке результатов.
Google Optimize и Stats Engine от Optimizely используют метод, а VWO недавно перешли на байесовские решения. И на то есть причины: подход осмысленный, ведь он отвечает на основной вопрос сплит-теста.
Байесовская статистика не использует нулевую гипотезу, но узнает: с какой вероятностью В лучше А? Так мы забываем о р-значении, вместо чего спрашиваем: учитывая наблюдаемые данные, какова вероятность того, что гипотеза верна?
То, чего мы ждем от тестов: В лучше А, или нет? И на сколько?
Байесовская оценка тестов
Подход избавляет от трудных терминов. Никаких нулевых гипотез, р-значений, z-значений и прочего. Байесовский метод просто показывает, что сработало лучше: В или А.
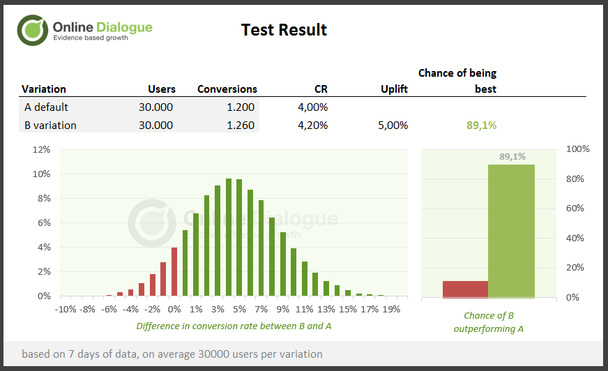
Звучит элементарно, не так ли? Посмотрим на график:
На основе данных метод показывает, что с вероятностью 89,1% версия В лучше, чем А. Используя байесовский подход, вы забываете о бинарности результатов. Теперь маркетологи видят точную цифру — на какой процент вариация лучше контрольной версии.
Больше не нужно твердить: «с р-значением 0.102 мы не можем отвергнуть нулевую гипотезу». Смело и громко заявляем: «С вероятностью 89,1% конверсия варианта В выше, чем у контрольной версии А!».
Второе звучит лучше, не правда ли?
Как появилось понятие о среднем значении?
Делайте ставки!
Но нужно ли реализовывать победившую версию? Байесовский анализ оценивает риски и рассчитывает, как результаты повлияют на доходы.
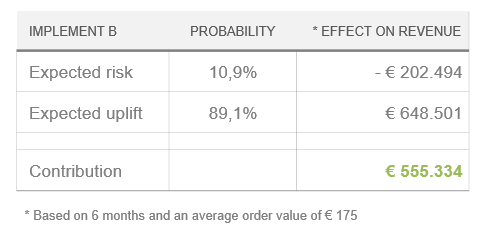
Среднее повышение дохода (сумма зеленых полос в примере выше) можно умножить на величину среднего значения и продлить период до 6 месяцев (примерно, потому что мы не знаем, как долго изменения будут стимулировать доход). То же справедливо для среднего падения конверсии (сумма красных полос выше).
В нашем примере, компания потеряет деньги с вероятностью 10,9% (сумма риска — около $ 200 тыс.), а заработает — с вероятностью 89,1% (около $ 660 тыс.). Заманчивая перспектива, не правда ли?
Байесовская оценка учитывает, что изменения могут быть незначительными, и проверяет, перевешивает ли ожидаемый рост дохода риски от нулевого эффекта.
Как далеко стоит заходить?
Разные типы компаний по-разному относятся к риску. Если у вас стартап, то пространство для маневра шире, чем у большого и «неповоротливого» бизнеса. Терять деньги не любит никто, поэтому минимальная вероятность успеха должна держаться на уровне 75%.
Число не фиксированное и может варьироваться, в зависимости от теста. Скажем, изменив заголовок, вы рискуете куда меньше, чем радикально переработав процесс заказа. На второе уйдет больше ресурсов, а значит, вероятность успеха должна быть выше.
Оптимизация конверсии и статистическая достоверность: что это значит?
Вместо заключения
На фоне частотной статистики, у байесовского метода целая россыпь преимуществ:
- Он понятнее — трудные термины статистики больше не нужны;
- Лучше подходит бизнесу — метод указывает, что В лучше А на Х%.
- Вы не теряете хорошие идеи, не доказавшие значимость при частотной оценке.
- Доходы растут, а изменения ускоряются. Вы не тратите время, опровергая нулевую гипотезу, а внедряете версии, которые принесут прибыль.
Высоких вам конверсий!
По материалам: conversionxl.com